CUBIC CIRCULAR
A quarterly newsletter for Rubik Cube addicts
Issue 1 Autumn 1981
| CONTENTS | | | |
| Welcome, Advertisement and Introduction | | 2 | |
| Ernő Rubik and his Cube | | 3 | |
| Cube Variations | | 5 | |
| Pyraminx - The Magic Tetrahedron | | 10 | |
| Clubs | | 12 | |
| Shortest Times and Competitions | | 12 | |
| Funny Moves | | 14 | |
| Errata to my Notes | | 14 | |
| General Anecdotes | | 15 | |
| Marital Anecdotes | | 16 | |
Published by David Singmaster Ltd., London, England. ISSN NO 0261-8362
2
WELCOME, ADVERTISEMENT AND INTRODUCTION
Welcome to the first issue of the CUBIC CIRCULAR. Let me begin by telling you my
plans for the Circular. Primarily it will be a newsletter to distribute information on the
Cube. However, there have been many new puzzles as a result of the enormous success of
Rubik's Cube™, and the circular will discuss these as well.
There has been so much interest in such puzzles and other mathematical puzzles, that I
have established a company to distribute them. I will use the Circular to announce
interesting new products as they appear, both from ourselves and from other sources. We are
always delighted to hear about new items for possible distribution and we maybe able to
organise production of them. Samples, drawings, patent specifications, etc. will be
gratefully received.
There has been a persistent demand for a newsletter like the Circular ever since the
fifth edition of my "Notes of Rubik's 'Magic cube'" appeared in September 1980.
As a consequence of the explosion of Cube mania at the beginning of 1981, I have been
receiving letters at several times the rate at which I can read and reply to them. Included
are manuscripts, books, computer programmes and computer printouts which can run to
hundreds of pages and require weeks to study! Consequently my study is piled with
unanswered correspondence and I would like to apologise to everyone who has written and
hasn't yet had a reply. I am hoping that the Circular will contain the answers to some of
the more standard questions and perhaps reduce the number of letters sent in by providing
the answer. The Circular may also be usable as a standard response letter.
Because much recent material In my study has not yet been properly read and filed, I find
myself sometimes remembering facts that I cannot relocate and so I am sometimes unable to
give proper credit to the source of an idea or fact.
I am delighted to receive copies of articles on the cube or related material - but
please be sure to put the date, name and place of publication on it. I would prefer
an original version rather than a photocopy, if at all possible. I would appreciate it if
you can include such details as the page number(s), transliteration and/or translation of
the title and/or abstract of the content for articles not in English, French, German or
Italian. Information on radio and TV items will also be appreciated - but again, please be
as detailed as possible.
At present, I have enough material to fill several Circulars - indeed, I am presently
preparing a bibliography which would fill several issues by itself! This issue contains
rather less than I had intended - all technical material has been deferred. Nonetheless,
I would be happy to receive short articles, news items, announcements, etc. for inclusion.
The Circular can be considered as further addenda to the fifth edition of my Notes which
is now being published by Penguin. A Spanish translation of my Notes by Gilberto Torbeck is
being published by Altalena Editores, Cochabamba 2, Madrid 16, Spain at 400 pesetas. A
German translation by Suzanne Bischoff will soon be published by Springer-Verlag, Berlin
& Heidelberg. A Dutch version is under way. We shall stock copies when they are
available. References to the Notes will be in the form N5, NS3, meaning page 5 and page
S-3 of the Notes. (In the American printing, pages i, ii became v, vi; pages S-1 to S-4
became 61 to 64, pages B-1 and B-2 were extended to 65 to 68 and I-1 to I-5 became 69-73).
I will refer to page 2 of Circular 1 as C1-2, etc. I will use the notation of my Notes since
it seems to be the most widely accepted of all notation. For typographic convenience, I will
abbreviate 3×3×3 as 33, etc.
I had hoped this circular would appear in early October. Apologies for the delay. I will
try to get the next circular done over Christmas.
3
ERNO RUBIK AND HIS CUBE
I have recently been informed by Cedric Smith that the symbol above the ő in Rubik's
first name is not an umlaut (") but a mark indicating a long o. This symbol is not
available on English typewriters and the attempt to produce it gives ö which is a
little odd looking, but acceptable.
Ernő Rubik was born in Budapest in 1944 to an eminent Hungarian family. His father,
Ernő Rubik Senior, was an aeronautical engineer who designed many gliders and was
awarded the Kossuth Prize (Hungary's highest honour). Rubik first studied sculpture,
matriculating from the Fine and Applied Arts Gymnasium in 1962 with a distinction in
sculpture. He then shifted to architecture, obtaining a diploma from the Budapest Technical
University in 1967. He then did a post-graduate diploma in interior architecture or
architectural planning (the sources vary - perhaps it was a joint course or the English
translations refer to the same subject?) at the Academy of Applied Arts. Upon completing
this course in 1971, he was appointed a lecturer at the Academy and began teaching
three-dimensional design among other subjects. He is now head of the studio for the study
of form.
Rubik found that his students, even the post-graduates, had great difficulty with
three-dimensional visualisation. Consequently he was thinking about various exercises for
his students. Cutting a cube with various planes is a fairly standard exercise and leads
to the well-known 23 and 33 arrays. Rubik has a life-long interest in
mechanisms, undoubtedly assimilated from his father. While contemplating the 23
and 33 arrays about May of 1974, this interest led him to ask, "How can I
make the faces move?" Within six weeks, he had a solution, first for the 23
and then for the 33 (which is much easier than the 23). It took him
a month to solve the cube when he made his first model. He applied for a patent on 30
January 1975.
At the end of 1976, he approached Trial, the major toy distributor in Hungary, and they
sent him to Politechnika Ipari Szövetkezet (i.e. Politechnika Co-operative), which
made plastic chess sets and similar games. Gyula Nemcsók, the chairman and co-founder
of Politechnika, recalls "When I took the Cube in my hand, excitement immediately
seized me. I took it to our chief engineer, who likewise recognised the fantastic
possibilities. We decided on the spot to obtain the necessary capital for production".
(My translation from A. Havas, Der Zauberwürfel, Wochenpost 28:23 [5 Jun 81].) By late 1977,
they could supply Trial. Trial made an initial order for 5,000 Magic Cubes (as they were
initially named) and anticipated that advertising would be required to sell them. Instead
they found that the problem was getting enough to meet demand. The Cube won a prize at the
Budapest International Fair in 1978, which led to a number of foreign orders. In 1978,
Hungarians were using the Cubes as hard currency which they could take or send abroad!
Hungarian customs officials now ask departing people "How many Cubes have you got?"
In 1979, the Cube received a prize from the Hungarian Ministry of Education and Culture. It
received the Toy of the Year awards for 1980 in the UK and Germany.
At the end of 1979, Ideal Toy, a major US and international toy firm best known for
introducing the teddy bear some years ago, took over the distribution for most of the
western world. They planned to call it 'The Gordian Knot' but someone came up with the
name 'Rubik's Cube'. I know no other toy named after its inventor - a unique tribute to
a unique invention! Ideal wisely spent time and money in retooling the production lines.
The resulting product is lighter, smoother in finish and much easier to turn. The original
Hungarian production, like much of the unlicensed Taiwanese production, was so stiff that
cubists developed 'Cubist's Thumb' or 'Rubik's Wrist'.)
The new version began to appear in mid-1980 and the resulting runaway success is now
well chronicled. Ideal sold about 4½ million Cubes in 1980 and anticipated sales of about
10 million in 1981. Although figures are not yet known for 1981, I estimate they have sold
perhaps 20 million so far. The Taiwanese are reported to have sold about three times as
many! There are reports of a Munich shop Selling 800 Cubes in an hour and of a Wolverhampton
(UK) shop selling 2000 in an hour. Market traders sold 1000 easily on Saturday. During the
great Cube famine of early 1981 when Ideal's stocks were completely depleted and the
Taiwanese knock-offs had not arrived, I heard of a second hand Cube market and offers of £15
for a Cube.
4
Rubik's name has become a household word in many languages and has been entered into the
Oxford English Dictionary and the Brockhaus Lexicon. UK Customs even has a new category:
Rubik's Cube and the like.
But what of Rubik himself? Early rumours said he was getting little royalties and he
still does not have a telephone. However, Ideal pays him a royalty on the use of his name
which has started arriving and recent reports describe him as the richest man in Hungary or
the first communist millionaire (though the currency is not specified). He receives between
1 and 2p per cube from Ideal and is said to be receiving about $30,000 per month after taxes!
He says it is just as well that he doesn't have a telephone.
The Cube is said to be Hungary's biggest single earner of foreign currency. With all the
production sent to the West this Eastern Block is almost unobtainable in the Eastern Block
Indeed an East German magazine has an article telling how to make your own Rubik Cube! Recent
reports indicate it is available and widespread in Poland
Rubik, his wife Rozsa and his 3 year old daughter Anna live in a hilly suburb of Buda in
a house he built with his own hands literally on top of his parent's house. His appearance
is more Mediterranean than Central European. He is of medium height, thin, with small neat
features. He has straight brown hair and smokes heavily. He reminds me a bit of Alain Delon
or Gerard Philipe. He is initially reserved but opens out when the conversation gets into
three dimensions. His conversation and manner are serious and intense. He often replies in a
way which opens up more questions and thoughts to consider. He is one of the few people that
I have met who immediately comes over as a genius.
Rubik consciously applied the fundamental principles of design when devising the Cube. In
particular, he aimed to make each piece as simple and compact as possible. He believes form
follows function. He is particularly pleased with the spring-loaded screws, which provide the
dynamic tension to hold the cube together and to take up wear. We have discovered several
earlier attempts to make Magic Cubes as well as several later independent designs. (Details
will appear in a later circular). The measure of Rubik's success at simplifying the mechanism
is that none of the other designs for the 33 has yet been produced.
Rubik has succinctly analysed the features of the Cube which made it unique among puzzles
when it appeared.
A. The pieces stay together.
B. More than one piece moves at a time.
C. The pieces have orientation as well as position.
I have written a section on the Fascination of Rubik's Cube for Rubik's forthcoming book
and have added some analysis of the more obvious points such as the three-dimensionality,
the coloration and the complexity. A point which I have recently realised, is that the Cube
has many subgoals - one can get pleasure out of simply doing one side or just the corners.
Like any masterpiece in any field, everyone can find his own special aspects of the cube to
fascinate him.
I have not yet been able to think of any previous puzzle with the three features Rubik
has pointed out. Now we have many variations and many new puzzles based on these points.
Perhaps we could now call them "Rubik's Rubric" for puzzle inventors.
CORRECTIONS - IMPORTANT
I gave a draft version of the Circular to Rubik on his recent visit to London. He has
pointed out a number of errors. I am afraid I depended on some published reports which were
erroneous. I am delighted to help set the record straight and must apologize for not
checking more thoroughly.
The ő in Ernő is actually a long ö.
Ernő Rubik Senior is still alive.
Rubik's subject is best called interior architecture.
Rubik approached Politechnika directly, not via Trial, about March 1975;
Gyula Nemcsók, the current president of Politechnika, was not president at that time
and was not involved in the first meeting with Rubik. (The details of the Havas
article seem to be all wrong.)
The 1975 prize from the Hungarian Ministry of Education and Culture was awarded to Rubik
personally for all his work. The Cube was also Toy of the Year for 1980 in France.
The retooling of the production in 1980 was entirely suggested and carried out by the
Hungarians. Ideal was
not involved. The stiffness and other problems with the earlier Hungarian production
were resolved in 1979.
Ideal's anticipation of 1981 sales has varied but the figure of 10 million was for the
US alone.
Royalties on the use of Rubik's name have not ever been agreed. Ideal buys all cubes for
Europe from Konsumex, the Hungarian export agency, and pays Konsumex a royalty on other
cubes made under licence. Rubik receives some royalty in both cases, but the monetary
values given are quite incorrect.
My contribution to Rubik's book has been used as the Foreword. In his book, Rubik
describes how he invented the cube at much greater length and with much greater authority
than I can do. The book will be available a month or two.
5
CUBE VARIATIONS
One of the marks of greatness which Rubik's Cube has demonstrated, is the ability to
inspire imitations and variations in profusion. The two most obvious variations have been
in the face patterns and in size. Most of the patterned cubes require one to solve the
supergroup (N 18, 22, 45). Patterns include magic squares, fruit, suits, die patterns,
chessmen, balls, O's and X's, and two types of Royal Wedding Cube - surely the ultimate,
symbol of 1981! One of these has nine identical pictures of each face: Charles, Diana and
flags of England, Scotland, Wales and the UK. The other is made in England and each face
is a single nine part picture: Charles, Diana and four Union Jacks. With the latter, you
can interchange the couple's hairdos or their ears! There are Cubes with the stickers
modified into circles or octagons and with glittery, pastel or grainy colours. Some cubes
have been used for advertising. Ideal is about to introduce a Calendar Cube with syllables,
letters and numbers allowing you to set the day, date and month on one face
This is an obvious executive toy which should keep the executive busy every morning.
Tamás Varga pointed out that one can modify the colour patterns on the Cube to
get a number of simpler Cubes. I have made up a number of these, of which the following
are the most interesting.
- All faces green - the Irish Cube (suggested by R. G. S. Hankin).
- 5 black faces, one white face - a Beginner's Cube.
- 3 yellow faces, 3 blue faces - with the yellows meeting at a corner.
(This is the pattern that Varga's colleague Julienne Szendrei showed me.)
- 2 opposite faces of red, white and blue.
- Remove the centre stickers.
- Remove the centre and edge stickers. This simulates the 23.
- Remove the centre and corner stickers.
- Remove stickers so the remainder form patterns like on a die or domino (suggested
by John Ergatoudis). One could also make such patterns using just white stickers on the
black cube.
- Make an all white cube and trace a continuous circuit through all the 54 facelets.
Finding such a circuit is a problem in itself. (Due to DBS based on a related picture in
Deledicq & Touchard's book).
Several of these patterns have indistinguishable pieces, which makes them easier at first
but can lead to complications later on. They are good tests of one's understanding of the
Cube.
EXERCISE. How many ways are there to put 1,2,..., 6 colours on the six faces of a
cube? The answer depends on whether you consider the actual colours as important or not and
whether one allows reflections or not.
EXERCISE. Find all the circuits through the 54 facelets.
Some South African students have just suggested some further patterns: the South African
Voters Cube - all white; the Bantustan Cube which starts with 5 black areas and one white
area and winds up with one black area and 5 white areas; a six coloured 13, called
the Total Apartheid Cube since the colours never get mixed.
A UK firm has produced a solid version of the Irish Cube called Rube Mick's Cube. A
number of other colour patterns are shown in the March 1981 Scientific American and the
October-November 1981 Jeux & Stratégie. In the latter, one version has all
stickers diagonally split between black and white. One could also use nine colours - one
of each on each face.
Stickers are now available to make each face a magic square on a gold background. This
is much harder than the previous magic square version which had different coloured
background. Dan Feldman sends a set of stickers from Israel but I'm not quite sure what one
does with it. I have seen a Do-It-Yourself Cube Kit which you assemble, but it has ordinary
stickers.
One can put one's own choice of pictures on a Cube. This requires careful cutting and
gluing. The result should be protected with some artist's fixative, but one must be careful
not to make the Cube stick together. Joe and Jamie Buhler put six playboy pictures on a
Cube for 3-D Jackson. He took hours to do it because it was all pink! Daniel Minoli sent a
pictorial cube with rather abstract pictures in only a few colours. He threatens to send
one with a short story in small print!
6
A Cambridge student, whose name I have forgotten, made white stickers with the same
letter along each edge so the letter could be read from each side as in the diagram. He
then found 6 3 by 3 letter patterns so that each row, column and diagonal is an English
3-letter word in one direction or the other. This gives 48 different words, though he says
there are 54 of them - perhaps some are words in both directions. Neil J. Rubenking suggests
labelling the 26 cubelets (or cubies) with the letters of the alphabet, trying to spell as
many 3-letter words as possible.
 |
There have been several inquiries about Cubes for the blind. (I also had an inquiry about
Cubes for the colour blind, but this has been solved by many of the patterned Cubes). Bernard
Morin, the well-known blind French topologist, used Dymo-Tape to produce tactile labels.
Rainer Seitz, the founder of the Rubik's Cube Club in Germany (of which more later), devised
the simple technique of using a hot needle to create craters in the plastic, in the form of
die patterns. One can do this oneself though it takes some practice to get the right size
needle, to get the right heat and to make the holes neat. Seitz demonstrated this technique
on German TV and about a thousand inquiries were received. He was subsequently proposed for
an award for services to the disabled. Cubes of this type and another type with brass studs
are now made in Germany and we can import them. James Dalgety, of Pentangle, says that some
may be produced here but so far I have no confirmation of this proposal.
The variations in size are more straightforward. The standard Rubik's Cube is 57mm
on an edge. Ron Leary, of the Mechanical and Production Engineering shops at my Polytechnic,
has produced some 114mm cubes in wood for demonstration purposes. I have recently seen that
cubes of similar size are being made in Germany, but I have no details. Commercially, one
can obtain cubes with edges: 52mm, 44mm, 38mm, 31 mm, 30mm, 27mm, 20mm. The smaller ones
come with key chains or neck chains attached to the cube or its package.
A different kind of variation has appeared. 23 cubes have been produced in
Japan. One type has Popeye characters on coloured labels and used Ishige's mechanism (N 37).
My example works very well, but Dalgety says his doesn't work so well. I gather this is no
longer being produced. Another 23 has a magnetic mechanism - each piece has a
magnet in it which holds it to a central steel sphere. Unfortunately, rapid turning causes
the pieces to come off. The outside of this version had all black labels with a silvery
path through the facelets, The path crossings are labelled so you know which end is matched
with which - leaving the labels off would have made a more interesting cube. Dalgety says
that Ideal will be bringing in a 23 soon. Jerry Slocum tells me he has three other
types from Japan. Wim Osterholt, a Dutch enthusiast, has made several types of 23
by hand and points out that the Rubik and Ishige mechanism are ends of a continuum of
mechanisms. Dan Sleator, now at Bell Telephone, made a 23 while a graduate
student at Stanford, which I saw in Summer 1980. His mechanism is like Rubik's, with one
additional point not specified in Rubik's patent. The theory of the 23 is
discussed in my Notes, especially N28, 29, 31. Solving it is quite easy, but there is one
point where you can go astray if your algorithm for the 33 does the edges before
the corners of the last layer.
7
Osterholt has built and patented a 43. He brought it to London and it worked
quite nicely once we lubricated it with Holt's rubber and nylon lubricant. Rainer Seitz
showed me some German patents or applications for 43 and 53. The
43 has 8 corners, 24 edges and 24 centres. If these are all distinguishable and
their orientations are noticeable, then we have
8!·24!·24!·38·224·424
= 4.8 × 1077 constructible
patterns. However, if we have each face a solid colour, then the edges occur in
indistinguishable pairs and the centres in quadruples, while the centre orientations are
unnoticeable. Thus we get only 8!·24!·24!·38·224
/ 212·246 = 2.2 × 1051 distinct constructible patterns
for the standard colouring. In the positions obtainable by layer turns, I have so far
determined that: i) each position must be an even permutation of the corners and centres
together; ii) the orientation of a corner is fixed by the orientation of the other seven
corners; iii) the orientation of an edge or centre is determined by its location. This gives
at most 8!·24!·24!·38 / 2·3 =
1.7 × 1055 patterns in the 43 supergroup.
If we use a standard colouring with solid faces, then we get to divide this number by
212·246 as above, to give at most 2.2 × 1043 distinct
patterns in the cube group.
Osterholt showed me a process which appeared to exchange one
pair of centres, though it is actually a 3-cycle with two centres indistinguishable.
Consequently, it looks like all the above patterns are indeed achievable by first getting
the centres correct, then the edges and corners by use of commutators of face layer turns.
Shape variations have also appeared. The simplest is a Truncated Cube, i.e. a Cube with
the corners trimmed off to leave 8 small triangles which are coloured gold (Figure 1). The
main Cube faces are thus octagons. The triangles are irrelevant so they can be coloured all
different. If one truncates further so the triangles just meet, one has a Cubo-octahedron
with 6 square faces and 8 triangular faces (see Figure 2 and the catalogue). This is sold
as a Diamond Puzzler. The corner pieces retain bits of the main cube faces, so the triangles
are still irrelevant, but they are coloured with 8 new colours. If one carries the truncation
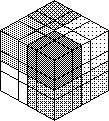
further until none of the Cube faces are left, one has an Octahedron which is dual to the
cube. The 8 triangular faces are coloured with 8 colours. A face centre of the Cube is now
a corner of the Octahedron, and has four colours on it. By adjusting the relative spacing
of the Cube's bisecting planes so the edge pieces are no longer cubical, we can make it so
that a corner of the Cube is now a triangular face centre of the Octahedron with only one
colour on it. The edges of the two shapes correspond, but the colour pattern behaves
differently on them (Figure 3). It is possible to simulate this Octahedron by colouring a
Cube with eight colours in a pattern looking like a 23 superimposed on the
33 (See Figure 4 or Scientific American, March 1981, p.15, bottom right picture.)
I call this a 'Dual' Magic Octahedron because the corners turn, rather than the faces. This
has been patented by Josef Trajber of Vienna and shown to me by Rainer Seitz. Its solution
is similar to the cube, but requires some new insights. It has
8!·12!·212·46 / 2·2·2 = 4.1 × 1019 = 40 50301 90700 29824
patterns. I don't know when this may be produced.
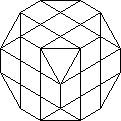 |
 |
| Fig. 1 |
Fig. 2 |
8
 |
 |
| Fig. 3 |
Fig. 4 |
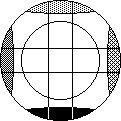
Another shape variation, which is still essentially a Cube, is the Magic Ball. This is
simply a rounded out Cube, approximately the circumsphere of a standard Cube, with diameter
about 95mm. The face centres are nearly square areas, but the edges are long rectangular
areas and the comers are large spherical triangular areas. The coloured stickers form large
circular areas about each face centre, tangent to one another, leaving some black area on
the corner faces - see the figure in the catalogue. Because you don't have the Cube's edges
to align the eye or hand as you turn, the Ball is quite difficult to do. A 75mm version
exists and miniature key chain versions of 31mm diameter exist. The latter have solidly
coloured faces, forming 8 columns of three like coloured pieces, with the North and South
Poles differently coloured or made to match one of the other 8 colours. There is also a
Magic Globe! An amazing combination of Geography and Geometry! Now you can sort out the
world! It comes complete with globe stand. At the time of writing these are not readily
available in the UK.
MAGIC BALL |
MAGIC GLOBE |
 |
 |
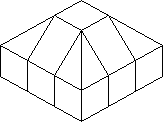
More interesting are shape variations which are not quite the same as the Cube. The first
of these was the Magic Octagonal Prism, which looks like a Cube with its four vertical edges
trimmed (Figure 5 and the catalogue). This gives eight vertical faces of three facelets and
two octagonal faces which are coloured with 10 colours altogether. The middle layer edge
pieces now have only one outside face, which means that you cannot tell which way round they
are. This makes the restoration easier at first, but harder overall since only half the ways
of putting in these pieces are possible when the rest of the Prism is restored. (Compare
with the comment of some of the patterned cubes). The colours of the vertical faces
corresponding to the trimmed edges are not related to the other colours, so they may be
rearranged, but again only half the ways are possible. In order to deal with these problems,
one must develop two further tricks beyond those used to restore the Cube. (I will give a
detailed solution in a later Circular). The Prism has only 1/8 of the distinct patterns of
the cube, i.e. 5406 50040 93112 32000 patterns and 12 of these can be considered as START
patterns. The Prism rapidly gets into non-convex shapes because it lacks cubical symmetry.
There are miniature Prisms with edges 37mm, 34mm, 30mm.
9
MAGIC OCTAGONAL PRISM |

Fig. 5 |
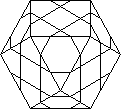
An odder shape is a Cube which is octagonalised along two axes (Figure 6). Mine is
labelled Million Space Shuttle on the two poles and I have heard it called a cushion or
pillow.
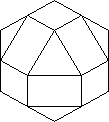
I have also recently obtained a Cube which has had all its edges and corners
trimmed to give 6 square centre faces, 12 rectangular edge faces and 8 triangular corner
faces (Figure 7). If the rectangles were squares, this would be a Small Rhombi-cubo-octahedron!
I will leave the detailed descriptions of these for a later Circular.
During a recent visit to Liverpool, Alexander Wall showed me an object he had created by
taking half of an Octagonal Prism and half of a Cube-octahedron and putting them together.
I suggest we call this a Chimerical Cube. Obviously there are slot of possibilities here
since almost all the standard size cube variations have the same internal dimensions. We
could even mix three or more kinds to produce the most amazing shapes!
I have recently put the catalogue of my cube collection onto a computer file, so it can
be kept up to date easily. Copies can be obtained by writing me with a stamped addressed
envelope or a mailing label and stamps or International Reply coupons appropriate for a
30gm or 1 oz letter.
I am delighted to receive samples of cubes, particularly those which I do not have.
Several people have sent examples in the past which I have not had time to acknowledge. My
thanks especially to Shiyusuke Nakamuraya who sent several samples from Japan which are not
available in Europe. I would be grateful for examples of any ancillary material as well,
especially the packaging, any enclosed leaflets and any advertising, posters, etc. which
can be sent.
 |
 |
| Fig. 6 |
Fig. 7 |
10
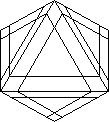
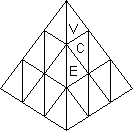
PYRAMINX - THE MAGIC TETRAHEDRON
All of the above described objects, except the 23, 43 and
53, are essentially variations on Rubik's basic idea. The first of the long
awaited other shapes has just arrived as a Magic Tetrahedron called Pyraminx (or Pyramix).
It is a tetrahedron trisected by planes parallel to each face (Figure 8). This gives 4
tetrahedral vertex pieces (V), 4 octahedral corner pieces (C) and 6 tetrahedral edge
pieces (E). The Pyraminx rotates on each of the trisecting planes. It has a ball bearing
action with detents to produce a smooth action and definite stopping. However, Pyraminx
has no face centres, so it is not easy to see just how it works. Basically, it is a 'Dual'
Magic Tetrahedron in that it is easier, although equivalent, to imagine the corners as
turning rather than the faces. I denote the faces by F, R, L, D and the opposite corners
by B, L, R, U. Part of the mystery of this pyramid is understanding how to orient oneself,
so I will say no more about it now. The Pyraminx is much easier than the Cube and it has
only 75582720 = 75,582,720 patterns, which can be reduced to 11,520 or even 960 patterns
of interest. EXERCISE. Derive these numbers. Consequently, it will bring great
joy to those who haven't been able to do the Cube. At the same time, it shows the basic
techniques which apply to all such puzzles.
| Fig. 8 |
 |
Pyraminx was invented about ten years ago by Uwe Mèffert, a Franco-German inventor
of scientific instruments. At the time he was interested in pyramids and the mysterious
powers they are reported to have. He found that running the point of a pyramid along the
palm relaxed him. Hence he wanted to make some kind of pyramid for the hand and the Pyraminx
was the result. It took him and his brother, a talented engineer, about two years to develop
the mechanism. When they completed their wooden model, they put it away and thought no more
about it. Mèffert only realised the potential of his idea after the great success of
Rubik's Cube last year. He showed it to several people in the puzzle field, notably To
m Werneck, and they were all enthusiastic, so he began to organise production this year.
Having seen the chaos in the Cube field, Mèffert has taken steps to protect
Pyraminx by means of patent, registered designs, trademarks and copyright in every relevant
country, especially in Taiwan and Korea which are not signatories of the international patent
conventions. He is already successfully enforcing his rights in Taiwan, although a number of
pirate versions of the pyramid have appeared in Europe, Australia and Canada, where he has
also been taking legal action successfully. An interesting further factor in his favour is
that he has used fluorescent orange PVC stickers for one face. This orange is a difficult
dye to use and only one firm in Europe can produce the material without using lead salts.
The Taiwanese versions are required to use Taiwanese produced material which contains about
5,300 parts per million of lead. The maximum amount of lead permitted under the UK Toy
Safety Regulations in a paint film is 2,500 parts per million and other countries have
similar or lower permitted amounts. The Regulations definitely refer to other types of
coating besides paint, so we believe the local authorities may be able to seize infringing
copies.
Incidentally, the Taiwanese 'knock-offs' are based on 21 examples stolen from
Mèffert's display stand at the Tokyo Toy Fair in June. By August, the Taiwanese were
advertising them for sale, complete with a defect that Mèffert had already corrected.
The Taiwanese versions are made from much inferior plastic and poorly finished, but are not
all that much cheaper than the original.
11
Mèffert has worked with an institution of the blind to produce a Pyraminx for the
blind with textured surfaces which are readily distinguished. These have been specially
coloured for the benefit of the partially sighted as well. Mèffert has developed
two simpler versions and two more complex versions of the Pyraminx, the most complex being
comparable to the Cube.
Kersten Meier, a computer scientist from Itzehoe, Germany, independently invented the
Magic Tetrahedron in 1980. He told me about it by telephone at Christmas, 1980, but I imagine
it looked like Figure 9 (I have recently learned that Peter Ruffhead, of Cambridge, applied
for a registered design for a tetrahedral puzzle of this form on 31 March 1981, and Ian Roger
James, of Potters Bar, applied for a patent which includes this design on 2 July 1981). But
Meier said that he could turn one corner and this did not agree with the results of Andrew
Taylor and of Uldis Celmins (N 29, 60). Subsequently, I extended and completed their results,
obtaining the number of patterns on any magic polyhedron. However, I then learned about other
face patterns from Rubik and later from a picture that Meier sent I did some of these, but
didn't get back to the Magic Tetrahedron until I heard reports of it from Jan van de Craats
and Tom Werneck in August and September.
| Fig. 9 |
 |
I have recently found a letter from Meier giving a solution algorithm which takes at most
33 moves and has an average of 20.2 moves. My own method takes 50 moves, which can be reduced
to 40 moves, at most. Mèffert reports a method that takes at most 38 moves and a newer
method that takes at most 30. Nicolas Hammond has used a computer to study the 960 essential
patterns and reports that any position is at most 21 moves from START. Further improvement
will require studying a larger set of essential patterns.
Two books on the Pyraminx have already appeared in Germany - one by Tom Werneck (now
published in English by Evans Publishers *) and one by Michael Mrowka and Wolfgang J. Weber
(which may appear in English as well). Werneck's book is more popular and has lovely colour
pictures of Mèffert, the production lines, diagrams, etc. But the Mrowka and Weber
book is more interesting for mathematicians, etc., giving a considerably easier algorithm and
more mathematical information. Mèffert is working with Professor R. F. Turner-Smith
of the Chinese University of Hong Kong on a "Book of Pyramids" which will cover
all the different Pyraminxes on both the popular and mathematical levels. This should be
appearing early in 1982.
Mèffert has already adapted his principle to an octahedron. Rainer Seitz has shown
me a number of German patents for other magic shapes and I think almost every variation has
now been considered. Some of these have even reached prototype stage and I have seen some of
these, but I don't know when any will become available. Rubik's Magic Domino (N34, 35) has
been redesigned and should appear in 1982.
* Mastering the Magic Pyramid by Tom Werneck. Evans, £1.50 (please add 15p for
postage if ordered from David Singmaster Ltd.)
12
CLUBS
Three national clubs have been formed.
Rubik's Cube Clube (Deutschland), Amselweg 12, D-6458 Rodenbach 2, Germany. (Founded by
Rainer Seitz).
Rubik's Cube Club (Schweiz), CH-4600 Olten, Switzerland. (Apparently an offshoot of the
previous club).
Japan Cubist Club, 3-D Daiichi Yazawa Building, 6-4-11 Roppongi, Minato-ku, Tokyo 106,
Japan. (Established by Tsukuda, the Japanese agents of Ideal).
Two regional clubs have been established.
Rubik's Cube Club Hamburg, c/o Peter Kellerman, Stormarnerstrasse 1, D-2000 Hamburg 70,
Germany.
Hasseltse Kubisten Federatie, do D. Durlinger, Genkersteenweg 179, B-3500 Hasselt, Belgium.
Three university-based clubs have been formed, at Bristol and Warwick in the UK and
Stanford in the USA, but I do not have current addresses for them. Many schools have set
up clubs, but I think there may be too many for us to record them in the Newsletter.
Nonetheless, I would be pleased to receive details of any clubs at all and I will certainly
list any national or regional clubs in future issues of the Circular.
SHORTEST TIMES AND COMPETITIONS
Single times for restoring a cube are not a good measure of ability, but it is amusing
to record them as an indication of the fantastic speeds which have been achieved. In my
Notes, the shortest known time was due to Nicolas Hammond, namely 36 seconds, Since then
Hammond has achieved it in 28 seconds (and perhaps less by now) and did 37 seconds on BBC
TV on 24 January 81. Nicolas is an upper sixth former (i.e. about 17 years old) at Nottingham
High School (UK). In Harburg, Hamburg, Germany, a 16 year old boy, Ronald Brinkmann, solved
his maths teachers cube overnight when the teacher finally gave up. Within a few months, he
did 29 seconds on German TV and later reached 24 seconds. When asked for advice, Brinkmann
replied, "Turn, turn, turn".
In Paris, Jérôme Jean-Charles, 25, has developed efficient ways of carrying
out processes, achieving an average of 36 seconds, then 32 seconds, within a minimum of 21.
He can do up to 180 moves per minute and can do (LF')63=I in 37 seconds. In
Bootle, Liverpool, Michael Musker, 16, a student at Hillside High School, has been timed at
20 seconds and says he once did 14 seconds when no one was watching. In Australia, Geoff
Harris, a 21 year old student at Griffith University claims he did a cube in 7 seconds! At
this point, the problem of deciding whether the cube was really in a random position becomes
apparent. Although any five or six moves effectively randomises the cube, some random
positions are much closer to START than others and this varies depending on the algorithm
used by the solver. Hence it is quite unreasonable to take single times. One should have
several gos and the cubes ought to be identical patterns for each person. Even then, as in
all sporting events, luck will still play some role.
Nicolas Hammond recently appeared on the Paul Daniels Magic Show and reports that Daniels
does the world's fastest cube - he throws it in the air and it comes down restored!
After the first competitions in Hungary (N38), the next major competition was on 31
January 81 at the Imperial Hotel in Tokyo, sponsored by the Japan Cubist Club. There were
400 entries and 73 passed the qualifying round. The contest consisted of restoring three
new cubes. The winner was a 16 year old schoolboy, Hideki Kitajima, with times of 62, 46,
49 seconds (average: 52 1/3 seconds). He won a new Datsun! Second prize was a Sony video
tape recorder, and there were three further substantial prizes. Kitajima said the new cubes
slowed him down - he usually does 25 to 30 seconds in his morning practice of 100 cubes.
13
Rainer Seitz organised a Guiness Book of Records bash in Munich on 6-13 March 81 at the
Olympia Shopping Centre. The Centre is connected with the German publisher of the Guiness
Book). The best times were 38 seconds, again due to new cubes, achieved by Ronald Brinkmann
and Jury Fröschl, an 18 year old Munich boy.
Ideal has begun a world championship, though it hasn't yet received much attention in
the UK, where the Daily Mirror is co-sponsoring it. Mal Davies (of whom more later) has
kindly passed on the first four (of eight) regional results.
| Edinburgh - Alex McNair, Edinburgh | 48.85 sec |
| Manchester - Edgar Whitley, Colwyn Bay | 39.98 |
| York - Brian Storey, Sunderland | 41.76 |
| Midlands - Nicolas Hammond, Nottingham | 35.38 |
| Bristol - Julian Bush, Bristol | 52.09 |
| Great Yarmouth - Julian Chilvers | 38.67 |
| Southampton - Christopher Lennon, Portsmouth | 55.35 |
| London (1st trial) -Ben Jones, St Nicholas-at-Wade | 46.12 |
| (In third position was Debbie Wade, fastest girl at 49.57; and in the lead
at lunch time with 61.71 sec was Benjamin Ealovega of Haslemere, Surrey, age 9, who says he
won't subscribe to Cubic Circular unless this is mentioned!) |
The rules allow a 15 second look at the Cube on a table. An automatic timer records the
time from when it is picked up to when it is set down. Only one trial is allowed in the
regionals, but there will be three trials at the final which will be on 12 December in
London. New Cubes are used which are described as randomised by a computer and contestants
pick one from a bin full. There will be a world championship in Monte Carlo next year.
The French national finals were held recently and Jérôme Jean-Charles won
with a time of 25.6 seconds. The New England regional was won by a 9 year old boy named
Jonathan Cheyer in 48.31 seconds.
The first Inter-school Rubik Cube Match was held on 15 October 81 between St Thomas
Aquinas RC School and The Holy Child Jesus School in Birmingham. There were 16 students on
each side. The fastest times were Anthony Shally (34 seconds) and John Bartlett (37 seconds).
The organiser was Mal Davies, a teacher at the first school, who was filmed giving a lesson
to his students and the TV station began the story that this was part of the regular
curriculum! Davies wishes to make it clear that such lessons are extracurricular. He has
started to teach an Adult Education class on the Cube! This takes three evenings and is held
at the Brasshouse Centre, Birmingham.
The youngest solver of the cube appears to be Lars-Erik Andersen, 7, of Lørenskog,
Norway. He does the cube regularly but cannot explain how. James Dalgety says an 8 year old
in Hampshire has solved the cube. Tanya Shelton, 6, in Oxford, has learned how to do the
cube from her father and is now much faster than he is.
Rainer Seitz reports that a boy in Germany does two cubes at once - one in each hand.
Mal Davies reports that Richard Hodson, of Queen Mary's Grammar School, Walsall, can do a
Cube one-handed in 89 seconds. John White, 19, a second year mathematics student at the
University of Warwick can do the Cube behind his back with one look. He demonstrated this
for Mal Davies, taking 10 minutes to study the Cube first. Unfortunately it came out with
two pieces wrong, which he then corrected behind his back, in a total time of 154 seconds.
14
FUNNY MOVES
Jérôme Jean-Charles has devised the following technique for implementing
(F2R2)3. Place your forefingers on the U sides of the UF
and UR pieces with your thumbs on the D sides of the DF and DR pieces. Figure 10 shows the
placing of the forefingers on the U face. One can now repeat F2R2
indefinitely without letting go! Jean-Charles also makes moves just flipping a corner piece
with a finger, e.g. B is achieved by flicking the D face of the DRB piece with the
forefinger.
Rainer Seitz makes a similar hold on the Cube, as shown in Figure 11. With this hold, one
can repeat L2B4L4B4L4... continuously.
Seitz calls this the Buddhist Prayer Wheel. Perhaps one should chant "Om Rubik om..."
or "Hare Rubik, hare Rubik, hare Rubik, hare, hare" while doing it.
Chris Strain-Clark holds her Cube similarly at the points shown in Figure 12. By skilful
slipping, one can carry out slice moves without appearing to have done anything at all. Pete
Strain-Clark points out that the group of patterns achievable is not a subgroup of the Cube
group because the orientation of the Cube is now important. Rather we have a subgroup of the
'oriented Cube group', which has 24N = 1.04 × 1021 elements.
ERRATA TO MY NOTES
The following are errata beyond the list of 23 Feb 1981, which were incorporated into the
American edition. The items on pages 37, 43, 44, 45, 49 are given on the list of 1 Jul 1981
which is included in the Penguin edition. The items on pages 46 and 51 are corrections to
previous errata.
Thanks to Frank Bernhart, Marston Conder, Sandy Frey, Jesper Gervaed & Torben Bisgaard,
Nicolas Hammond, Colin Merton and Anneke Treep for finding some of these.
Page 21, Line 21. In the antislice notation, the second process is (FR)3U2.
Page 37, Line 5; Page 38, Line -2; Page 51, Line -14; Page I-3, Left, Line -6. Change Nicholas to Nicolas.
Page 43, Line -6. Change to: L'U'B'U2BLUFU2F'.
Page 44, Line -16. Change to: (MBT&KO - 9)
Page 45, Line -7. Delete: (See also .
Page 45, Line -3. Change to: (MBT - 14).
Page 45, Line -1. Change to:RaF2aR'a·U·RaF2aR'a·D'
Page 46, Line 30. ... only moves (A, C-)D- in ...
Page 49, Line -6. Insert:(UF, DL).
Page 50, Lines -15-14. The first non-obvious case is 88 which ... have 8 and 11 cycles...
Page 51, Line 26. Change the total to 355995.
Page 51, Line 31. Change to: 3389 45406 22394 = 3.39 × 1013.
Page 51, Line 32. ... about 7.84 10-7 ...
15
GENERAL ANECDOTES
Fred Warshofsky relates that a football game in Connecticut was delayed due to a
missing player who was discovered playing with his Cube in the locker room. Someone told me
of a UK court being disrupted by a Cube. Several people have told me that the Cube reduced
the productivity of their department to zero. One in London and one in Washington pointed
out that because they worked for government departments, one couldn't notice the difference.
Paul Samet, head of the University College London Computer Centre, bought a copy of my Notes
so he could get his staff back to work.
An Italian engineer in Nigeria, Vittorio Burgatto, won a Chinese dinner for two when the
proprietor saw his Cube and said it looked easy! Robert Cole told me that two people followed
him out of a waiting room into his train compartment when he was playing with his Cube.
Fifteen minutes later one of them realised he was on the wrong train.
Ideals promotion of the cube in the US started with a party given by Zsa-Zsa Gabor in
Hollywood on 5 May 80 (N37), followed by a New York do on 8 May 1980 with three generations
of Gabors. In Hollywood, Solomon W. Golomb, the inventor (or at least the popularizer) of
Polyominoes™, appeared as the mathematical half of the sponsorship. David Sibley was
the mathematician on the East Coast. Miss Gabor managed to forget the name of the product
at the Hollywood press conference.
English Cube-mania (Cubanoia?) began when Rubik appeared on Swap-Shop, a Saturday morning
BBC TV children's programme on 24 January 81, along with Nicolas Hammond, who did the Cube
in 37 seconds. They had several other bits on the cube in the preceding and succeeding
weeks, and at later times. The competing show, in ITV, Tiswas, has just launched a 'Stamp
out Cubes' campaign. Songs have been written about the Cube! "Mr. Rubik" by the
Barron Knights is available in the UK on Epic EPC Al596. (See the catalogue).
. There is an
Australian song and a German one by a character called Krazy Kuno.
Rubik's Cube has become a household word - I have seen it used as a metaphor in
political, educational and economic contexts as well as in numerous political and humorous
cartoons. The first political cartoon was by Felix Mussil in Frankfurter Rundschau on 5
February 81, reprinted in Stuttgarter Zeitung and Der Spiegel. It showed a bemused
Chancellor Schmidt with a Cube labelled Berlin, unemployment, etc. On 7 July, Garland did
a cartoon in The Daily Telegraph showing Willie Whitelaw and Maggie Thatcher struggling
with a Cube labelled racial violence, etc. On 6 September, I saw Reagan's Cube by Paul
Conrad of the Los Angeles Times reprinted in The New York Times Weekly Review. It had 27
problems showing! A Mahood cartoon In Punch for 9 September shows The Russian Cube - an
enormous cube being parachuted onto troops - "A variation of the Rubik Cube, this
game is guaranteed to drive any enemy to distraction within minutes". Numerous other
cartoons and even a poem have appeared.
Hamlet Cigars have used the Cube for two commercials. One shows my hands getting a Cube
all correct, then it is turned to reveal a blue centre in the white face, whereupon It is
dropped in disgust Another uses another pair of hands just to show increasing frustration
with the wretched thing, then dropping it.
Several people have discovered their Cubes have moved when they left the house, the
only people about were children or workmen who swore they hadn't touched it. Hence we
have concluded that either there are poltergeists (which explanation I cannot accept) or
the Cube must be able to move by itself. This led one correspondent to wonder if one could
force theCube to surrender, he thought of starving it, but he couldn't work out what it
ate. He then tried sensory deprivation - keeping it in its box in a dark drawer - but to
no avail.
There is a definite mysteriousness about the Cube. There is a hotly denied rumour that
one of John Conway's graduate students got his beard caught in a Cube and was slowly pulled
into it despite his friends' efforts. It is thought that he will reappear when the Cube is
returned to the same position it was in when he was first trapped, but no one noticed what
it was. CCC (N 30), which is better denoted as C3, has commandeered all the
computers in Cambridge to run through Cube patterns in hopes that the desired pattern will
be recognisable, perhaps by the appearance of the missing cubist on the video screen. The
German advertising for the Cube says 'Do not take hold of it - it will not let you go'.
How prophetically true this is - or is it a warning subsequent to a similar Germany tragedy?
16
There has even been a Cubic Communion. The Reverend Richard Ames-Lewis conducted this at
Edenbridge Parish Church on 25 October 81. When I first heard about this, I supposed that
his parishioners needed holy help to restore their Cubes, but he says he used the Cube as
an image of disorganised life which one is presenting for God's grace. Still, I'm sure some
people were secretly hoping their Cubes would come back solved.
The mixture of religion and cubism may be an interesting development.
Solomon Golomb has devised an analogy between Cube corners and quarks, which he has extended into a complete
Cubic cosmology. (More on this and on naked beauty or bare bottom in a later Circular).
A correspondent has recently written that the Cube has allowed him to come out of the
closet, the mathematical closet, that is. In the past, when he told people he was a
mathematician, they treated him like a social outcast. Now they ask how to do the Cube.
Beautiful blondes come up to him in airports asking him to relieve their misery, etc.
So many books have come out on the Cube (details in a larger Circular) that Pan Books
is about to publish 'Not Another Cube Book'.
 |
"And he's at it all night too!" |
MARITAL ANECDOTES
Rainer Seitz told me of a Cube-caused divorce case last March. He has kindly sent
the report from Bild Zeitung, which is datelined Bottrop, Ruhr region, 27 Feb (1981). A 21
year old salesgirl was complaining that her husband no longer spoke to her, fled from
visitors, never watched TV and no longer did anything in bed. Seitz volunteered to act as
marriage counselor by teaching him how to do the Cube, but nothing came of it.
Seitz also reported that a woman with a large black eye came to a demonstration. Her
husband had got two faces correct and she had disturbed it while he was at work She had
been given two days to get it right again!
A later report comes from Kassel, "She dreams of sex, he only dreams of six
sides". 'I have gone nearly mad, being woken up at six by that stupid klick-klack'
complained Ilse K. (33) about her technician husband Otto K. (36). He replied that he bought
the Cube as a present for her, because she didn't like flowers.
One a more positive note, Eric Pfisterer (the same one), a schoolteacher in Toronto, says
that a girl he had known as a child, now grown up, came to Vienna with a Cube and promised
to marry him if he solved it He did and she did! And they are living happily ever after.
In England, Pete Strain, a lecturer at the Open University and a world-class racing
cubist with a best time of 21 seconds, met a girl, Chris Clark, at summer school and they
found the Cube a mutual fascination. He promised to marry her when she got down to 60
seconds. She did and he did! (Actually she was already down to 70 seconds, so this wasn't
so great a challenge as it seems). They are now Pete and Chris Strain-Clark Her two
daughters also do the Cube and they are claiming a family record! I gave their name to some
media people and they volunteered to do the cube underwater! This was filmed for Anglia TV
but I gather all you could see was bubbles. They had facemasks but were holding their
breath. Chris' face mask got flooded so she had to complete her cube by memory.
I mentioned the divorces and marriages in a talk I gave to the British Association on 4
September 1981. This got headlined as 'Cube Route to Divorce', etc. Next week Private Eye
did a pseudo-Sun front page with "Exclusive - How 'That Cube' can improve your love
life - Harvard Prof. Tells All".
© David Singmaster
The text and original drawings are copyright © David Singmaster, reproduced here with
permission. Conversion to html and additional commentary by Jaap Scherphuis.