Kep Korong / Rubik's Cheese

The Kép Korong (Picture Disc) is a predecessor of the Hockey Puck, and has the same mechanism but with fewer pieces. It has the shape of a thick disk. In the centre are two semicircular parts, and around these are 6 segment pieces. The centre can rotate with respect to the segments, and one of its halves can be given a 180 degree turn to change the order of the segments. Each side has a picture of a cartoon character. A neat feature is that in its solved state the centre must be out of alignment to complete the pictures. It is extremely rare and hard to find.

The Kép Korong was invented by András Végh, a Hungarian physicist. He filed a patent, HU 184418, on 01 April 1981 which was granted on 30 June 1987.

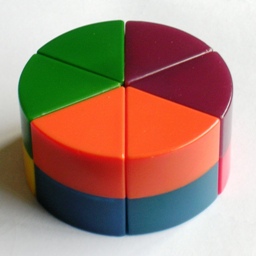
Rubik's Cheese is a predecessor of the Rubik's Ufo, and has the same internal mechanism except that it has only one layer instead of two. It is quite a rare and expensive puzzle. It is essentially the same puzzle as the Kép Korong, except that it has no rotating centre, so any three adjacent segments can turn at all times. Each segment has different colours on top and bottom, and in the solved position each side of each piece shares its colour with a piece next to it. The solved position therefore shows three colours on each side of the puzzle. The picture above shows the version where there are three identical pairs of pieces, but it is more common for the pieces to have six different colour pairings so that in the solved position the three coloured regions of one layer do not coincide with the three regions of the other.

The US patent for Rubik's Cheese was filed on 9 November 1981 and granted 18 October 1983, US 4,410,179, but its first patent is the Hungarian patent HU180612, filed 9 November 1980.

The number of positions:

The pieces come in two sets of three which cannot intermingle. In fact, the Rubik's Cheese has a mechanism where three pieces are fixed on axes connected to a centre core, while the other three pieces are held between them. Each piece has two possible orientations, so at first sight there are at most 3!·2⁶ = 384 positions. This limit is not reached because the number of flipped pieces of each set of pieces has the same parity as the permutation parity of the other set. This leaves only 3!·2⁴ = 96 positions for the Rubik's Cheese.

The Kép Korong also has two centre pieces which should be taken into account. They seem to have 2·2 ways they can face, but due to a parity restriction there are really only 2 cases for any given position of the pieces. This means there are 96·2 = 192 positions, or if the rotation of the centres matters, 192·6 = 1152 positions.

The following table shows how many positions there are for each number of moves:

Depth	Cheese	Kép Korong
0	1	1
1	3	6
2	6	13
3	12	24
4	18	36
5	24	48
6	23	46
7	9	18
Total	96	192
Avg Depth	4.625	4.635

In Sloane's On-Line Encyclopedia of Integer Sequences the Rubik's Cheese sequence is included as A079830.

Below is a table setting out how many Kép Korong positions there are for each number of moves when centre rotations are counted as moves as well. It shows that it can be solved in 14 moves (9.3576 on average) and if every 60 degree turn of the centres counts as a separate move it takes at most 15 moves (10.359 on average).

	Total	1	6	10	30	41	48	64	96	112	120	144	168	160	108	44	1152
		Face turn metric
S i x t h t u r n m e t r i c		0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	Total
	0	1															1
	1		3														3
	2		2	4													6
	3		1	4	6												11
	4			2	10	8											20
	5				9	16	12										37
	6				4	12	24	16									56
	7				1	4	12	32	24								73
	8					1		16	48	28							93
	9								24	56	30						110
	10									28	60	36					124
	11										30	72	42				144
	12											36	84	40			160
	13												42	80	27		149
	14													40	54	22	116
	15														27	22	49

Notation:

Mentally label the segments/pieces of the disk clockwise from A to F. Any twist of three segments can then simply be denoted by the letter of the middle segment of those three.

Solution:

Phase 1: Orient the pieces

If there are any three adjacent pieces of which two or three are flipped, then twist that half.
Repeat step a as often as possible.
If there are still pieces flipped, for example piece A, then do CDE and turn over the puzzle. If necessary, repeat until no flipped pieces are left.

Phase 2: Arrange the segments

Consider pieces A, C, and E correct, and compare pieces B, D, and F to them. To cycle around B->D->F, do the moves CDECDE. To go in the opposite direction B->F->D do EDCEDC.

Phase 3: Fix the centre (Kép Korong only)

During the last move done in the previous phases, you can always ensure that at least one half of the centre facing the correct way. Due to parity, the whole centre should then be facing the correct way. If you have to turn over the centre anyway:
Do any move (i.e. turn over one half)
Rotate the centre 180 degrees
Turn over one half again.
Rotate the centre until the picture on the front is correct.

Jaap's Puzzle Page

Kép Korong / Rubik's Cheese

JavaScript Rubik's Cheese

The number of positions:

Notation:

Solution: