


The Kibble Cube consists of 27 cubes on an elastic string. The cubes have grooves in them which allow the elastic to be positioned so it enters the cube in one of three cube faces, and exit it from one of the three other faces. The cubes are coloured, each side a different colour, similar to a Rubik's Cube. The aim is of course to arrange the string of cubes in a large 3×3×3 cube, with each side a single colour.
The puzzle is closely related to the snake cube puzzles, but differs in that the elastic can enter/exit different faces of the small cubes, and that you not only have to make a large cube, but that the colours on the sides have to match as well.
I don't know who designed the Kibble Cube, but a similar puzzle was patented by Giorgio Giorgi on 25 June 1986, EP 185,628.
Let me define a position as any 3×3×3 arrangement, regardless of the colours. If the string makes a turn at a cube, then there are 8 ways that cube can be oriented, but if the string goes straight through there are 12 ways of orienting the cube. The two end cubes also have 12 orientations. If we know how many unique ways there are for the string to pass through all 3×3×3 cubes, and know how many 90 degree turns there are in each, then we can count all the positions. When analysing the Snake Cube I already counted all such string arrangements, except that in that case reversing the path of the string was considered the same. As the Kibble cube's colouring is not symmetric from one end to another, path reversal results in a different set of positions. Running a slightly adjusted version of the computer program resulted in the first column in the table below.
| Straights | Strings | Pos. per String | Positions |
|---|---|---|---|
| 2 | 24 | 12 4823 | 293,768,974,166,354,889,453,600,768 |
| 3 | 235 | 12 5822 | 4,314,731,808,068,337,438,849,761,280 |
| 4 | 1037 | 12 6821 | 28,559,852,457,235,314,409,067,249,664 |
| 5 | 2563 | 12 7820 | 105,880,764,485,864,191,172,284,514,304 |
| 6 | 3444 | 12 8819 | 213,413,979,451,414,128,597,745,532,928 |
| 7 | 2674 | 12 9818 | 248,549,207,775,732,308,305,910,956,032 |
| 8 | 1159 | 1210817 | 161,594,165,190,018,929,689,538,592,768 |
| 9 | 303 | 1211816 | 63,368,893,942,073,859,830,798,352,384 |
| 10 | 46 | 1212815 | 14,430,540,204,630,680,951,567,941,632 |
| 11 | 2 | 1213814 | 941,122,187,258,522,670,754,430,976 |
| Total | 11487 | 841,347,026,476,462,627,955,970,932,736 |
Thus there are about 8.41·1029 ways of folding the puzzle into a 3×3×3 cube. Of these, it turns out that there are 288 solutions, though they are all minor variations of each other.
The solution is essentially unique. There are variations due to the fact that the centre cube can have any orientation, and some of the cubes at face centres can be reoriented without changing the only visible colour. Furthermore, the front and back layers can be swapped, like a kind of mirror image, as can the left and right layers.
Below is a picture of the solution.
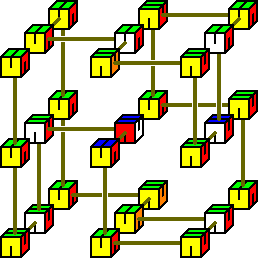
There now follows a text description of this solution.
There cubes have two colour schemes on the cubes, which are mirror
images of each other. They always have blue and green on opposite
sides, as well as red opposite orange, and white opposite yellow.
If you carefully examine the colour scheme of the cubes starting at
one end of the string, you will find that the first three or five
cubes are identical before encountering a mirror image scheme.
Start with the end that has 5 identically coloured cubes. Arrange them
so that their blue and green faces touch, and their sides match. The
first cube will be the front top left corner in the 3x3x3 arrangement,
with the next two cubes directly underneath it. They must have either
white or yellow at the front (both lead to a solution).
I'll use the letters F,L,U,B,R,D for the directions Front, Left, Up,
Back, Right, and Down. Starting at the previously mentioned front top
left corner, the string of cubes then goes in the following directions:
D D B U R F D R B L B L U U F R F R D B U B L D R D
The last cube is at the back bottom right corner.
When analysing/solving this puzzle by hand, there are some ways in which you can drastically reduce the search. First of all, like the snake cube puzzles, if you number the cubes from 1 to 27, the odd numbered ones including the two ends must lie at the corners and face centres of the eventual 3×3×3 cube. When you examine the colouring of these 14 cubes, you find that 4 of them have a mirror image colouring compared to the other 10. Since the eight corners must have the same colouring, these four must lie at face centres.