Jaap's Puzzle Page

Mad Triad

Mad Triad Handy Mad Triad

The Mad Triad puzzle (also called the "Twisting Tri-Side Puzzle" in the UK) consists of intersecting discs of 6 (rounded) triangular tiles each which can rotate. There are two versions. The "Handy" and the "Challenge".

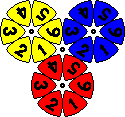
The "Handy" Mad Triad has three separate discs - red, blue and yellow - arranged in a triangle. In the centre two tiles from each of the three discs form a fourth disc which allows the pieces to be mixed properly. This handy version is in a casing in the shape of a hand, where each finger twists to turn a disc. The tiles of each colour are numbered.

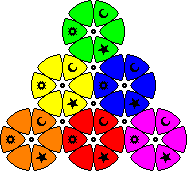
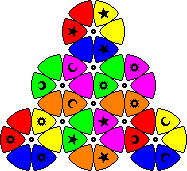
The other version is the Mad Triad Challenge, and it has 6 coloured discs - green, red, yellow, orange, blue, purple - again arranged in a large triangle. Wherever three discs come together, an extra disc is formed by two tiles of each. There are four such extra discs, making ten all together. They can be rotated by twisting a knob in the centre of each disc. Three of the tiles of each colour have a symbol, a moon, sun or star. Several different patterns are shown on the box and the instructions which you can try to make.

For such a seemingly simple puzzle, it has an elaborate mechanism that locks the tiles in place. Without it the rounded triangular tiles would no doubt twist or slide out of arrangement. When you begin to turn a knob, the transparent upper casing is lifted to release the tiles, while another unseen part is raised underneath and locks the tiles onto the axle. It is highly ill-advised to take apart a Mad Triad. It has many intricate parts and some springs, which makes it difficult to put back together again. There are good reasons for the casing to have 7 screws to keep it together.

This puzzle is closely related to the Turnstile puzzle which has similar intersecting discs. It was invented by Heng-Chun Ku, and the patent was granted on 8 February 2000, US 6,022,021.

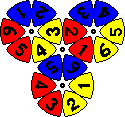
Some patterns for both puzzles are shown below. These are taken from the packaging of the puzzle, though I have slightly altered some to be more symmetric.

The Three Wheel The Triple Crown
The Three Wheel The Triple Crown
The Pin Wheel The Half & Half The Mid Wheel
The Pin Wheel The Half & Half The Mid Wheel
The Six Wheel The Multi Wheel The Colour Wheel
The Six Wheel The Multi Wheel The Colour Wheel
 
The Split Wheel The Zig-Zag Wheel The Pin Wheel
The Split Wheel The Zig-Zag Wheel The Pin Wheel
 
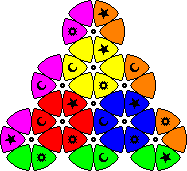
The Stripe Wheel The Centre Stage Wheel The Kaleidoscope Wheel
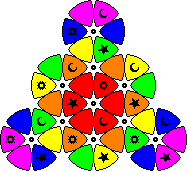The Stripe Wheel The Center Stage Wheel The Kaleidoscope Wheel
 
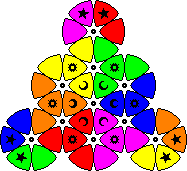The Criss Cross Wheel The Triangle Wheel The Border Wheel
The Criss Cross Wheel The Triangle Wheel The Border Wheel

The number of positions:

The "Handy" Mad Triad has 18 tiles, which can therefore be arranged in at most 18! permutations. All these can be attained. Each tile has 3 possible orientations. Like the Rubik's Cube, the total orientation twist of the puzzle is and remains zero throughout, so that the orientation of one tile depends on the other 17. Therefore there are actually 18!·317 = 826,803,583,944,627,953,664,000 distinct positions. Note however that there are 36 solutions, as there are 6 colour arrangements, and the discs can all be rotated the same amount.

The Mad Triad Challenge has 36 tiles, which can therefore be arranged in at most 36! permutations. All these can be attained, but as 3 tiles of each colour are indistinguishable, there are only 36!/3!6 = 7.97·1036 visibly different arrangements. The marked tiles also have a visible orientation - this is most noticeable on the moon symbol, but the star and sun symbols can be rotated such that one point is directed towards the centre of its disc. There are therefore 318 possible orientations, giving 36!·318/3!6 = 3.1·1045. If you ignore the symbols completely, then there are 36!/6!6 = 2,670,177,736,637,149,247,308,800 positions.

Solution:

Most of the puzzle can be solved relatively easily, but at the end when there are only two unsolved intersecting discs it suddenly becomes much more difficult. Some useful move sequences are shown below. The notation of the moves is straightforward - L and R denote clockwise turns of the Left and Right discs respectively through 60 degrees, i.e. one single step. Anti-clockwise turns are denoted by L' or R'.

A. 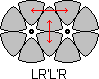Two swaps - LR'L'R B. 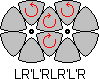Four twists - LR'L'R LR'L'R C. 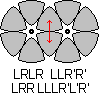One swap - LRLR LLR'R' LRRLLL R'L'R' D. 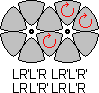Three twists - LR'L'R LR'L'R' LR L'R'LR L'R

Note that sequence B is just A repeated twice. Sequence D can be remembered as sequence B R' B' R (where B' means the inverse of sequence B). Sequence C will simply have to be memorised as it stands on its own.

Phase 1: Solve everything except for one disc.

If you have two intersecting discs, L and R, it is fairly straightforward to solve the outer part of the Right disc, i.e. the four pieces that do not lie in the L disc. A description is given below. If you can do this, then you can easily solve the Mad Triad except for a single disc, simply by working from the outside inwards, each time solving those sections that are part of only one unsolved disc.

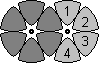Suppose you have two intersecting discs, L and R, then the following steps will solve the outer section of the right disc. In the description the four piece positions are numbered clockwise from 1 to 4, i.e. position 1 means the top position of the right disc, and 4 the bottom position.

  1. Find the piece that belongs at position 4. Bring this to the middle, orient it with respect to the Right disc, and bring it to position 2. This is quite easy as there are no solved pieces yet that need to be maintained.
  2. Find the piece that belongs at position 3. Put it correctly oriented in position 1 as follows:
    1. Bring the piece to the left disc without disturbing the previously placed piece. In particular if it lies at position 3 or 4, then do RRLLR'R', so that it lies in the left disc.
    2. Put the piece at position 1 (if it isn't there already) by turning L so that it lies at the top of the left disc and doing move sequence A (LR'L'R).
    3. If the piece is at position 1 but not correctly oriented, then do sequence B (LR'L'R LR'L'R, which is sequence A twice).
  3. Do R, so that the solved pieces lie at 2 and 3.
  4. Find the piece that belongs at position 2. Put it correctly oriented in position 1 as follows:
    1. If it lies at position 4, then do RLR', so that it lies in the left disc.
    2. Put the piece at position 1 (if it isn't there already) by turning L so that it lies at the top of the left disc and doing move sequence A.
    3. If the piece is at position 1 but not correctly oriented, then do move sequence B.
  5. Do R, so that the solved pieces lie at 2, 3 and 4.
  6. Find the piece that belongs at position 1.
    1. Put the piece at position 1 (if it isn't there already) by turning L so that it lies at the top of the left disc and doing move sequence A.
    2. If the piece is at position 1 but not correctly oriented, then do move sequence B.

Phase 2: Position the pieces of the last disc (orientation ignored).

Let the last unsolved disc and an adjacent (intersecting) disc be Left and Right discs respectively. To swap any two adjacent pieces on the Left disc, turn the Left disc so that the two pieces to be swapped are in the middle, do move sequence C, and turn the Left disc back again. Using such adjacent swaps it is fairly easy to put all the pieces of the Left disc in the right order. Note that sequence C changes the orientation of some pieces in the Left disc, but does not disturb the four solved pieces of the Right disc.

Phase 3: Orient the pieces of the last disc.

  1. Find any piece in the Left disc that needs to be twisted.
  2. Turn the Left disc so that the twisted piece is at the bottom right, i.e. adjacent to piece 4 of the right disc.
  3. Do move sequence D to twist the piece. If it is still not oriented correctly, then do sequence D again. (Instead of doing D twice, you may also do the inverse of D.) Note that pieces 1 and 2 of the Right disc will twist as well, but ignore that.
  4. If there are any pieces in the Left disc that still need to be twisted, go back to step a.
  5. Turn the Left disc to the correct position. Note that pieces 1 and 2 of the Right disc should have automatically ended up in the correct orientation again.