Jaap's Puzzle Page

Moeraki Games Nr. 4

Pyraminx Duo Pyraminx Duo 6-colour

Pyraminx Duo is a puzzle in the shape of a tetrahedron, consisting of four corner pieces and four triangular face centre pieces. Each corners can be rotated, and when doing so the adjacent face centre move along with it. At the start, each face has a single colour and the aim is of course to restore this state after it has been mixed.

The puzzle was invented by Oskar van Deventer. He wanted to make the simplest possible non-trivial twisty puzzle, where a puzzle such as the Morph is considered trivial because after the first move there is no choice in subsequent ones.

The second picture above shows a version with custom stickers that make the orientations of the face centres visible. This makes it a bit more difficult.

The number of positions:

There are 4 face centres which can be permuted in at most 4! ways. The corners can twist independently of each other, and each has 3 possible orientations giving them 34 possible states. This gives a total of at most 4!·34 = 1,944 positions. This limit is not reached however because of some constraints. You can consider the face centres to be the faces of a smaller tetrahedron. Every move merely rotates this tetrahedron. This already shows that it is impossible to swap two centres as that would not result in the mirror image colouring of the tetrahedron rather than a rotated one. We can also define the twist number for any orientation of a tetrahedron as shown in the following diagram.
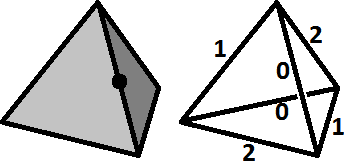
Twist of a tetrahedron
One of the edges of the tetrahedron shown on the left is marked. Whichever orientation this tetrahedron is given, the associated twist number can be determined by finding where its mark is, and looking at what number this edge is given in the wire diagram on the right. You can easily check that any clockwise rotation abouy a corner of the tetrahedron will cause the twist number to increase (modulo 3) and that an anti-clockwise rotation causes a decrease (mod 3).
Every clockwise move on the Pyraminx Duo increases the twist number of the tetrahedron formed by the face centres, and also increases the twist of one of the corner pieces. Therefore the total twist of the corner pieces must be equal to the twist of the centre tetrahedron.
The total number of positions of the Pyraminx Duo is therefore 4!·34 / (2·3) = 324.

Suppose the orientation of the face centres is made visible. Each face centre has 3 orientations, potentially multiplying the number of positions by a factor of 34. However, each clockwise move twists one corner but also twists one face centre relative to the inner tetrahedron. Therefore the total corner twist must be equal to the total twist of the face centres relative to their tetrahedron. This means the orientation of one face centre is determined by the rest of the puzzle and there are only a factor 34/3 times as many positions. There are therefore 4!·38 / (2·32) = 8,748 positions when centre orientation is visible.

No Centre
Orientations		With Centre
Orientations
Depth#positions
01
18
248
3188
479
Total324
Avg Depth3.0370
Depth#positions
01
18
248
3288
41,436
54,286
62,636
745
Total8,748
Avg Depth5.0609

Links to other useful pages:

Meffert's puzzles Uwe Mèffert's site. He invented the Pyraminx and now produces and sells the Pyraminx Duo amongst many other puzzles.

Solution:

  1. Twist the corners until they match each other. Note that any two corners share two colours, and must be turned so that both of these shared colours line up.
  2. If the centres are not yet solved, hold the puzzle so that you see only two faces with only two colours all together, i.e. two faces which need their centres swapped. Hold the puzzle by the two nearest corners, the corners shared by the aforementioned two faces. Then do the following moves:
    1. Turn one of the two corners clockwise.
    2. Turn the other corner anti-clockwise.
    3. Turn the first corner back, anti-clockwise.
    4. Turn the other corner back, clockwise.

If you have visible face centres, also do the following steps.

  1. Find two face centres that need to be twisted, preferably in opposite directions.
  2. Hold the puzzle by the two corners that are opposite the two twisted centres.
  3. Do these moves:
    1. Turn one of the two corners clockwise.
    2. Turn the other corner anti-clockwise.
    3. Turn the first corner back, anti-clockwise.
    4. Turn the other corner back, clockwise.
    5. Turn one first corner anti-clockwise.
    6. Turn the other corner clockwise.
    7. Turn the first corner back, clockwise.
    8. Turn the other corner back, anti-clockwise.
    This will have twisted one centre clockwise (the one nearest the first corner you turned) and the other centre anti-clockwise. If both the centres are still not solved, then repeat the moves exactly.
  4. Repeat the steps c-e if necessary until all the face centres are correctly oriented.