Row by Row

Row by Row is a puzzle manufactured by Tomy. It consists of an array of 6 rows which
each can contain 7 round pieces. There is one blank space, so there are 6·7-1=41
pieces. Tilting the puzzle left or right causes the pieces in the row containing the
blank space to slide to the left or right. The pieces cannot slide up and down because
the rows are separated by thin walls. The left or right column of the puzzle can be
moved up one row, or down one row (so both columns have three positions - up, centre,
and down). Shifting these columns allows the pieces and the blank space to change rows,
and mix the puzzle up completely. There are 6 pieces of each of the colours brown,
green, blue, yellow, red, and orange, and 5 uncoloured (transparent) pieces. In the
solved position the transparent pieces are in right (or left) column, while the
remaining parts of the rows have one colour each.
The puzzle was invented by Mizunuma Masanori and Watanabe Hiroyuki, and patented
by Tomy on 13 November 1984 (filed 7 May 1982), US 5,389,063. That patent also covers Tomy's
Rack 'em up puzzle.
If your browser supports JavaScript, then you can play the Row by Row by clicking
the link below:
The number of positions:
There are 6·7=42 pieces (including the gap), giving a maximum of 42!
arrangements. Positions that differ only by column shifts will be considered
identical. The limit of 42! is not reached because:
- There are six sets of six of indistinguishable pieces (6!6)
- There are five indistinguishable transparent pieces (5!)
- The blank is generally in the left or right column (6/2)
This leaves 42!/(3·5!·6!6) = 28,014,361,976,725,689,202,886,081,433,600
= 2.8·1031 positions.
Notation:
Tilting the puzzle to the left or right, i.e. shifting the pieces of the row containing
the blank to the left or right, is denoted by the letters L and R. Moving up the left
or right column is denoted by Ul and Ur, and similarly moving them down by Dl and Dr.
Solution:
In this solution the transparent pieces will end up in the right hand column, with
the blank space above it. I will therefore assume that at the start, and between
each of the steps of the solution, the blank space will also be in the right hand
column, and that the two columns are in the central position.
Useful moves:
Here are a few short move sequences, and their effects. They form the basis of the
solution. Note that the sequences on the right are the inverses of those on the left.
| 1a. R Dr L Ur |
 |
| 2a. R Ur L Dr |
 |
| 3a. R DlDr L UlUr |
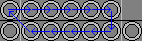 |
| 4a. R UlUr L DlDr |
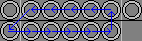 |
| 5a. Ul R DlDr L Ur |
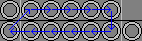 |
| 6a. Dl R UlUr L Dr |
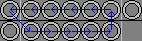 |
|
| 1b. Dr R Ur L |
 |
| 2b. Ur R Dr L |
 |
| 3b. DlDr R UlUr L |
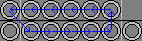 |
| 4b. UlUr R DlDr L |
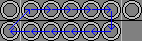 |
| 5b. Dr R UlUr L Dl |
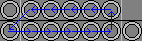 |
| 6b. Ur R DlDr L Ul |
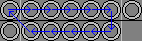 |
|
Phase 1:
Solve the bottom row.
- Find a transparent piece.
- Manoeuvre it into position on the right hand side of the row you are solving. This
is fairly straightforward:
1. Use sequences 1 and 2 to move the gap to the same row as the piece.
2. If necessary use 3a to shift the piece to the right, into the sixth column.
3. Use sequences 1 and 2 to move the piece down to the row above the one
you are solving, still in column 6.
4. Do 1b, and 2b to put it in place.
- Decide on the colour that you want the row you are solving to be.
- Find a piece of the right colour, which lies in a different row.
- Manoeuvre the piece into column 6 in the row above the one you are solving.
- Apply 4b to shift the piece into the row.
- Repeat steps d-f until the row is solved.
Phase 2:
Solve the next three rows.
Use the same method as in phase 1 to solve the second, third and fourth row from the bottom.
Phase 3:
Solve the last two rows.
- Use 3 or 5 to move the final transparent piece into column six, and then
use 1 and 2 to put it into the last column of the second row from the top.
- Decide which colours the first two rows should have.
- Use 3 or 5 to put as many pieces in the correct rows as possible.
- If the first piece of the first row is incorrect, and the second row has an incorrect piece
that does not lie in the first column, then
1. Do 3a until the incorrect piece from the second row is in the first column.
2. Do 5b equally often, so that most of the pieces are back to where they started.
Both incorrect pieces will move to the other row.
- If the first row has an incorrect piece that does not lie in the first column, then
1. Do 5b until the incorrect piece from the first row is in the first column.
2. Do 3a equally often, so that most of the pieces are back to where they started.
Now go back to step d.
- If the second row has an incorrect piece that does not lie in the first column, then
1. Do 3a until the incorrect piece from the second row is in the first column.
2. Do 5b equally often, so that most of the pieces are back to where they started.
Now go back to step d.
- If the leftmost piece of each of the first two rows are incorrect then do 3b and 5a.


