The loop shift transform

1. Fold the magic along its length into 1×n rectangle.
2. Pull it apart to get one long loop of tiles. If you do not get a loop, then go back and fold the 2×n rectangle over in the other direction to get the 1×n rectangle.
3. Fold the loop flat at any point (the drawings below shift the loop along only one tile).
4. Fold the magic open again to get back to the rectangle shape.

Note that if you open the loop an odd number of tiles away from where you started, the puzzle folds out upside down.

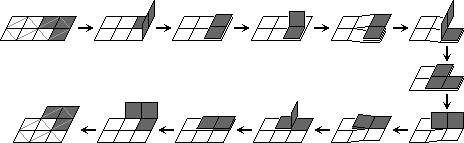
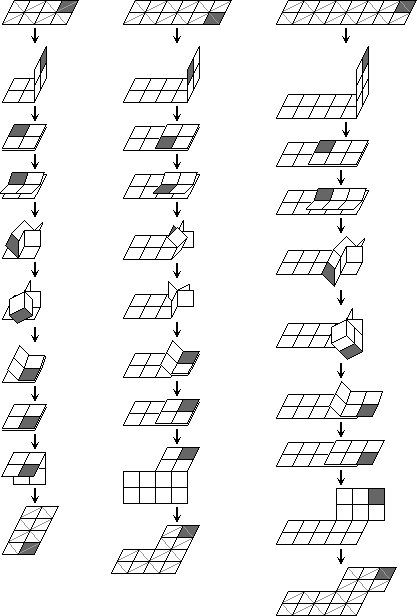
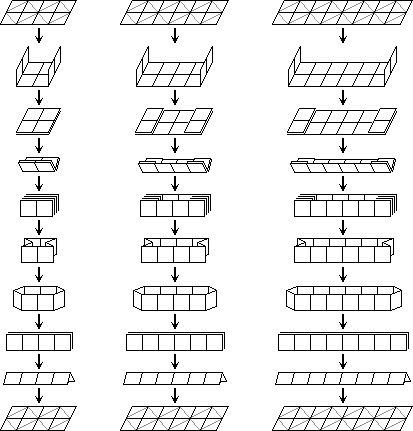
The star shift transform

1. Fold the 2×n rectangle up in zig-zag fashion to a block.
2. Now peel off one tile from the top half and turn it over onto the bottom half. If this is not possible, then go back to the beginning and fold the 2×n rectangle up in the other direction and try again.
3. Fold the tile on the other side of the bottom half up to the top half.
4. Now unfold the puzzle back to the rectangle shape.

The name I've chosen for this transform is due to the fact that when the puzzle is folded up into a block, the tiles can be peeled off and spread out into the shape of a star.

On the longer magics (2×6 or longer), it is not necessary to completely fold up the puzzle, allowing for the following quicker version.

The rectangle transform

1. Fold the leftmost column of tiles rightwards onto their adjacent tiles, and similarly fold the rightmost column of tiles left onto their adjacent tiles.
2. Fold the back tiles of the top row upwards, and similarly the back tiles of the bottom row downwards. If it cannot unfold that way, then go back to the start, turn the puzzle over and try again.
3. On the standard 8-tile magic you are finished now. On larger magics, fold the left hand column and right hand column back inwards under the adjacent tiles.
4. Fold the front tiles of the top row upwards, and similarly the front tiles of the bottom row downwards.
5. On the standard 12-tile magic you are finished now. On even larger magics, repeat the steps starting from step a.

The interesting thing about this transform is that it turns a horizontal rectangle into a vertical one. If you then hold the rectangle horizontal again, it has the effect of rotating all the tiles a quarter turn.

The six-flip shape changing transform

There is one indispensible transform needed to solve these puzzles. This transform changes the shape of a 2×4 rectangle to a 3×3 square with one corner missing, i.e. from a rectangle to a V shape.

1. Hold the top right tile of the rectangle and fold it (and also the tile below it) leftwards onto the adjacent tiles.
2. Fold that tile downwards. If this is not possible, start the whole thing again but with the other side of the puzzle facing you.
3. Fold that tile (and the one above it) leftwards.
4. Fold that tile (and the one to its right) upwards.
5. Fold that tile rightwards.
6. Finally, fold that tile (and the one to its left) upwards.

Note that only three tiles are moved by this transform. Learn to do both the mirror image and the inverse of this transform.

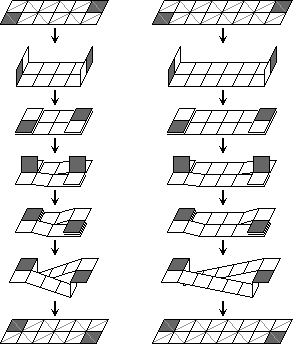
The twist transform

This is a strange transform that is extremely useful. It looks very neat, and if you want to solve the Magic very quickly will work well. However, it can put more strain on the wires than the other transforms used so far, so make sure you do it accurately. Note that the drawings below show three slight variations of the move.

1. Fold the right hand side 2×2 square leftwards on top the other tiles. (In the Super Magic drawings a variation is shown where 6 tiles are folded over.)
2. Pull up the top and bottom edges of the left two of those tiles so that they hinge two form a V shape.
3. Rotate those two tiles anti-clockwise through 180 degrees. (In the Master Magic drawings a variation is shown where the tiles are rotated clockwise instead.)
4. Fold out the bottom layer of the tiles to make a flat shape again. (In the Super Magic drawings the top layer is folded open instead.)

I did not find this transform myself, but once saw someone solve Rubik's Magic on TV using it.

The row swap transform

This transform swaps the two rows of the magic. This can also be done by using the star shift transform followed by the loop shift transform, both times moving the same tile to the other row

1. Fold the leftmost column of tiles rightwards onto their adjacent tiles, and similarly fold the rightmost column of tiles left onto their adjacent tiles.
2. Fold the puzzle along its length so that the previously folded tiles go on the inside.
3. Unfold those inner tiles, so that the puzzle forms a loop. If this is not possible, retrace your steps and start the whole thing again but with the other side of the puzzle facing you.
4. Pull the loop flat, so that the tiles that where inside have been inverted and form the ends of the 1×n rectangle.
5. Now unfold the puzzle back to the rectangle shape.