Jaap's Puzzle Page

Slide Rule Duel: Pie 3 and Pie 6

Slide Rule Duel Pie 3 Slide Rule Duel Pie 6

These Slide Rule Duel puzzles have pieces which in the top half of the frame form two large circle segments, and in the bottom half only one small circle segment. The bottom half can slide left and right so that its segment can line up with either of the top parts to make a complete disc, which can then be rotated. Pie solved positions

The Pie puzzles have discs cut into 8 pieces like a pizza. There are only three half-discs, so there are 12 pieces all together. The Pie 3 has three colours, four pieces of each colour, and the Pie 6 has six colours, two pieces of each colour. In the solved position the pieces of the same colour are together, forming three half discs, or 6 quarter discs.


These puzzles were invented by Douglas A. Engel, who also invented various other puzzles such as:

The number of positions:

There are 12 pieces which can be arranged in 12! ways, but there are indistinguishable pieces so we have to divide out by the number of ways the identical pieces can be permuted, which is 4!3 for the Pie 3 and 2!6 for the Pie 6. This gives 12! / 4!3 = 34,650 positions on the Pie 3, and 12! / 2!6 = 7,484,400 positions on the Pie 6. If you consider a position different if the slider is moved across, then you have to multiply these numbers by 2.

I have used a computer to calculate God's algorithm for these puzzles. The results in the table below show that any Pie 3 position can be solved in at most 8 rotations (5.5990 on average), or 13 (9.7245 on average) if every 1/8th of a turn is counted as a separate move.

Face turn metric
S
i
n
g
l
e

t
u
r
n

m
e
t
r
i
c		 012345678Total
0:11
1:44
2:4812
3:4161636
4:224502298
5:2410010424252
6:1613428618614636
7:81445227181881,580
8:21107421,788889443,575
9:496783,0382,9482226,935
10:123643,1905,5541,066210,188
11:2941,4964,9962,074208,682
12:41861,1951,170142,569
13:44036282
Total:114986172,81610,63015,8244,6123834,650
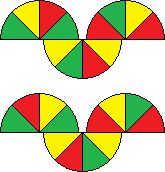
Antipodes of Pie 3

There are two positions that are antipodal in both metrics, which are shown on the right. They can be reached with the move sequences R3 L2 R2 L1 R3 L-2 R-2 L1, and L3 R2 L2 R1 L3 R-2 L-2 R1. In a sense they are mirror images of each other, as you can see from the similarity between the two move sequences.

The Pie 6 can be solved in at move 11 rotations (8.6679 on average), or 19 times 1/8th of a turn (14.779 on average).

Face turn metric
S
i
n
g
l
e

t
u
r
n

m
e
t
r
i
c		 01234567891011Total
0:11
1:44
2:4812
3:4161636
4:2244828102
5:249612840288
6:1613431627862806
7:8144560896540922,240
8:21207882,0002,1629731206,165
9:708323,3766,0244,7961,52612016,744
10:306044,37512,27216,2039,3701,6862444,564
11:63884,37619,29040,22839,18412,752504116,728
12:11303,20423,51277,172121,12866,1944,464295,805
13:1,70421,982115,934290,380250,25926,19428706,481
14:54614,911131,371525,850699,737107,5441741,480,133
15:1006,65098,198632,7661,298,898296,8627192,334,193
16:1,34635,864359,9311,163,775417,5451,4111,979,872
17:523,32851,060271,224161,7821,192488,638
18:165825,1405,65219311,583
19:235
Total:114986653,77420,895108,803524,1752,031,8973,769,7871,020,5743,7177,484,400

Links to other useful pages:

PuzzleAtomic is Douglas Engel's site. You can order these puzzles there.

Notation:

Hold the puzzle with the slider at the bottom. The Left and Right discs will be labelled by the letters L and R. A turn of a disc is denoted by the disc letter followed by a number that is the number of steps to turn it by, where positive numbers mean clockwise turns, and negative numbers anti-clockwise turns. So for example L2 is a clockwise quarter turn of the left disc, and R-1 is an anti-clockwise turn of the right disc by one step, one eighth of a full turn.

Solution to Pie 3:

Phase 1: Solve the top half of the left disc.

  1. Choose which colour you want the top half of the left disc to be. I'll assume it to be red in the steps below.
  2. Place a red piece at the left hand side of the top left half disc.
  3. Move the slider to the right.
  4. Rotate the right disc until a red piece lies at the left of the slider's half disc.
  5. Move the slider to the left.
  6. Rotate the left disc clockwise one step to add the red piece to the top half.
  7. Repeat steps c-f until all four red pieces lie in the top half of the left disc.

Phase 2: Solve the second disc.

  1. Rotate the right disc until it matches one of the patterns in the table below. Then do the associated optimal move sequence to solve it.
    Right discSolution
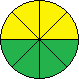    YYYYGGGGDo nothing
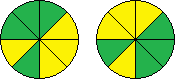    YYYGGGYGL-2 R1 L-1 R-1 L3
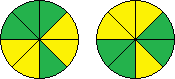    YYYGGYGGL-1 R1 L-1 R-1 L2
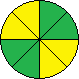    YYGGYYGGL1 R-3 L-1 R-2 L1
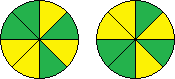    YGYYGGYGL2 R1 L3 R1 L2
    YGYYGYGGL-1 R-1 L-3 R-1 L-3
    GYGYGYGYL-2 R3 L1 R1 L1 R2 L-2

Solution to Pie 6:

Phase 1: Solve the top half of the left disc.

  1. Choose which two colours you want the top half of the left disc to be. In the steps below I'll assume it to be grey at the top left, and red at the top right.
  2. Place a red piece at the left hand side of the top left half disc, but such that the other red piece does not also lie in that half disc.
  3. Move the slider to the right.
  4. Rotate the right disc until the second red piece lies at the left of the slider's half disc.
  5. Move the slider to the left.
  6. Rotate the left disc clockwise one step to add the red piece to the top half.
  7. If there are grey pieces in the top left half disc, then turn the right disc so that there is no grey piece in its top half, and do L2 R2 L-2.
  8. Move the slider to the right.
  9. Rotate the right disc until a grey piece lies at the left of the slider's half disc.
  10. Move the slider to the left.
  11. Rotate the left disc clockwise one step to add the grey piece to the top half.
  12. Repeat steps h-k for the second grey piece.

The following move sequence swaps the two pieces lying in the top right quarter of the right disc:
   L1 R2 L-1 R-2 L2 R1 L-2 R-1
The second disc can be solved with this sequence alone.

Phase 2: Solve the second disc.

  1. Choose a piece to use as a reference point. This piece will be considered already solved, and all the other pieces will be solved relative to this piece. If you already have two pieces of the same colour that are already next to each other, use the pair of them for reference instead.
  2. Examine the piece or pieces that are already solved, and determine which piece belongs clockwise immediately adjacent to them.
  3. Rotate the right disc so that the piece you want to move lies at the right of the top right half disc.
  4. Apply the move sequence mentioned above to shift the piece one place anti-clockwise, bringing it closer to the block of solved pieces.
  5. Repeat steps c-d until the piece is adjacent to the block of solved pieces, and so is itself also solved.
  6. Repeat steps b-e until all the pieces are solved.

If you want to rearrange the colours of the Pie 3, any permutation is easily achieved using half turns only. To rearrange the colours of the Pie 6 however, just using quarter turns is not enough. This is because this problem is equivalent to permuting 6 corners of the Rubik's Cube using only moves of two adjacent faces. The page about the Two-generator corners group explains the mathematics of it.

Two swap two adjacent colours of the Pie 6, rotate them to the bottom, into the slider's half disc, and do the move sequence:
   L2 R-3 L1 R3 L-3 R3 L1 R3
Then move the two colours back to where they were before.